Tags:    c++
Vektor Klasse

3D grafik er baseret på vektor matematik. Hvis du aldrig har arbejdet med dette emne før så fortvivl ikke. Vi vil lave en ganske almindelig vektor klasse, som kan de mest basale funktioner med nogle enkle tilføjelser. I første omgang behøver du ikke at kunne forstå, hvad disse funktioner rent faktisk gør. Først når vi skal til at simulere realistisk lyskilder, vil du få brug for at forstå det.

En geometrisk vektor repræsenterer en retning, men den kan også opfattes som blot et punkt i et 3-dimensionel rum. Når der tænkes på et punkt bliver vektoren ofte kaldt for en vertex. En vektor skal derfor bestå af mindst tre komponenter, der hver repræsenterer henholdsvis akserne X, Y og Z. I mange sammenhænge vil disse tre komponenter være nok til at dække de fleste behov, men da vi i forbindelse med 3D ofte gerne vil arbejde med 4x4 matricer vil vi få brug for homogene koordinater. Homogene koordinater har tilføjet en fjerde komponent som kaldes enten for W eller H (Homogeneous). Den fjerde komponent repræsenterer ikke en akse på samme måde som de tre første gør. Den homogene komponent er egenligt bare en skalér der har effekt for de resterende komponenter. Det vil vi komme ind på senere.

Siden vi gerne vil opnå en nøjagtig placering af vores vektor, bliver vi nødt til at bruge decimal tal til at reprænsenter vores fire komponenter. Computeren kan tilbyde to typer decimal tal, hvoraf den ene er mere nøjagtig end den anden. Vi snakker selvfølgelig om float typerne: double og single. Float typen: double, er mere præcis end float typen single, men den er også lidt langsommere. Man kan sagtens bruge dem begge, men da vi er mest interesseret i præcision fremfor hastighed, vil vi nok få mest gavn af float typen: double.

Som tidligere nævnt skal vores vektor klasse kunne de mest grundlæggende ting som f.eks. at lægge to vektor sammen, men den bliver også nødt til at havde en mere fremtrædende funktion. Da de mest almindelige 3D modeller er bygget op af trekanter, skal den kunne finde en skæringspunkt i en trekant. En trekant har selvfølgelig tre kanter, derfor må den også bestå af tre punkter. Som nævnt tidligere kan disse punkter opfattes som tre vertex'er eller tre vektorer. Derfor vil det være meget naturligt at placere en sådan funktion i netop vores vektor klasse.

Der findes mange algoritmer der kan finde en skæringspunkt i en trekant. Nogle er bedere end andre, alt afhængig af hvilke informationer man ønsker omkring skæringspunktet. I vores tilfælde har vi behov for en hel del information. Først skal vi vide om vores skæringsvektor rent faktisk har en skæringspunkt i en given trekant eller ej. Hvis den har en skæringspunkt, skal vi vide, hvor henne på trekantens flade punktet befinder sig. Vi skal også vide, hvor punktet befinder sig i henhold til eventuelle tekstur (texture) koordinater. Vi vil også gerne vide om vores skæringsvektor skærer forsiden eller bagsiden af trekanten.



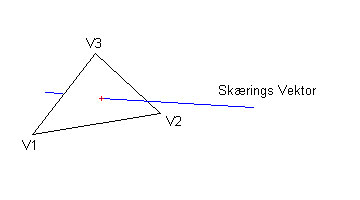
Som du kan se på illustrationen ovenover, har vi en en blå skærings vektor og en trekant der består af vektorne V1, V2 og V3. I dette tilfælde skærer vores vektor trekantens flade, men det er let at forestille sig en situation, hvor en vektoren ikke ville skære trekanten. Samtidig kan du se at vektoren går igennem trekanten fra den nærliggende flade, som vi kunne kalde forsiden, og går ud gennem trekantens bagside. Hvorfor er det vigtigt at vide? Det vil blive vigtig for os, når vi kommer til at skulle beregne lysets fald. Desuden er det ikke sikkert du overhovedet ønsker at rendere bagsiden. Der kan opnåes visuelle effekter ved ikke at rendere den.

Den nok mest kendte algoritme er Möller & Trumbore's klassiske skæringsalgoritme fra 1997. Den er designet til Raytracing og er blevet testet af mange forskellige programmører gennem tiden. Det eneste negative man kan sige om denne algoritme, er, at den er relativ langsom. Men du vil nok ikke kunne finde mange algoritmer, der kan levere så mange informationer som denne og samtidig være stabil. Denne artikel vil ikke beskrive, hvordan selve algoritmen fungere. Hvis du er interesseret i disse oplysninger, findes der et hav af artikler på nettet som du kan læse. Derimod vil vi fokusere på, hvordan vi kan aflæse de relevante informationer og bruge dem i vores program.

Möller & Trumbore's skærings funktion kalder vi for: Intersect, da er det engelske ord for det samme. Den skal som sagt skrives i vores vektor klasse. Her er funktionens prototype:

    unsigned char Intersect( VECTOR & RayNear, VECTOR & RayFar, VECTOR & V1, VECTOR & V2, VECTOR & V3,
                             const bool TwoSided = true,
                             const double DepthTest = 10000 );

Lad os kaste et hurtigt blik på, hvilke værdier funktionen kan returnere og betydningen af dem.
Funktionen kan returnere værdierne 0, 1 eller 2:
0 = Funktionen har IKKE har fundet en skæringspunkt.
1 = Skæringspunkt er fundet på forsiden af trekanten.
2 = Skæringspunktet er på bagsiden af trekanten.

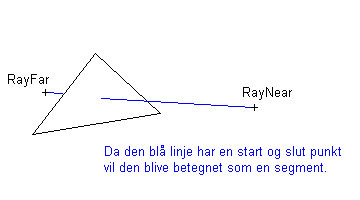
RayNear og RayFar vil tilsammen udgør en segment. Som tidligere nævnt kan en vektor opfattes som at være en retning eller et punkt. Skæringspunktet kan ikke findes ved blot en retning. Vi skal vide hvor linjen starter og hvor den slutter. Vi kunne antage at startpunktet altid vil ligge i koordinat nul. Altså, hvor X, Y og Z alle tre er lige præcis nul og dermed bruge vektorens koordinater som slutpunktet. Når du engang kommer til at implememtere skygger og specielt reflektioner, vil du finde ud af at samme algoritme kan bruges, men du vil få brug for at ændre startpunktet. Derfor er det bedst at havde en startpunkt og en slutpunkt defineret som to separate vektorer.



V1, V2 og V3 er alle vektorer der tilsammen udgør en trekant. Parameteren: TwoSided, vil afgøre om bagsiden af en trekant skal ignores eller ej. Den sidste parameter: DepthTest, angiver ganske enkelt den tilladte dybde. Som regl har den samme værdi som RayFar vektorens Z komponent men den skal altid havde en positiv værdi. Hvis trekanten er længere væk end, hvad denne parameter tillader kan den ignoreres.

Selve skæringspunktet, hvis der altså er fundet en, vil blive gemt i vektor klassens X, Y og Z komponenter. Dog er det ikke de geometriske koordinater der er tale om.

X og Y komponenterne vil indeholde barycentriske koordinater. Disse kan også opfattes som UVW koordinater, altså trekantens fysiske tekstur (texture) koordinater. Vi vil ikke komme til at bruge W komponenten i denne artikel men den kan omregnes ganske enkelt: ( 1 - U - V ) eller ( 1 - X - Y ).

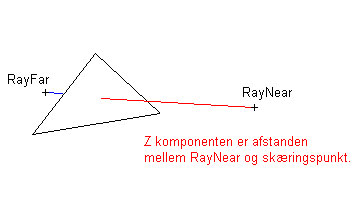
Z komponenten er afstanden mellem RayNear og RayFar. Den geometriske skæringspunkt kan derfor findes ved at trække RayFar fra RayNear, for denæst at gange resultatet med Z komponenten og til sidst lægge det hele til RayNear vektoren:

Skæringspunkt = RayNear + ( RayFar - RayNear ) * Z

Vi kan bruge funktionen FollowLine til denne udregning.



Vektor klassen vil komme til at se således ud:

#include <stdlib.h>
#include <math.h>

class VECTOR
{
  public:
    double X, Y, Z, W;

    VECTOR( void );
    VECTOR( const double X, const double Y, const double Z, const double W );
    void SetValues( const double X, const double Y, const double Z, const double W );
    void SetValues( const double X, const double Y, const double Z );
    VECTOR Add( VECTOR & V );
    VECTOR Sub( VECTOR & V );
    VECTOR Mul( VECTOR & V );
    double Dot( VECTOR & V );
    void Cross( VECTOR & V1, VECTOR & V2 );
    double Magnitude( void );
    double Length( void );
    double Length( VECTOR & V );
    void Normalize( void );
    unsigned char Intersect( VECTOR & RayNear, VECTOR & RayFar, VECTOR & V1, VECTOR & V2, VECTOR & V3,
                             const bool TwoSided = true,
                             const double DepthTest = 10000 );
    void FollowLine( VECTOR & V1, VECTOR & V2, const double Distance );
};

VECTOR::VECTOR( void )
{
  X = 0;
  Y = 0;
  Z = 0;
  W = 1;
}

VECTOR::VECTOR( const double X, const double Y, const double Z, const double W )
{
  this->X = X;
  this->Y = Y;
  this->Z = Z;
  this->W = W;
}

void VECTOR::SetValues( const double X, const double Y, const double Z, const double W )
{
  this->X = X;
  this->Y = Y;
  this->Z = Z;
  this->W = W;
}

void VECTOR::SetValues( const double X, const double Y, const double Z )
{
  this->X = X;
  this->Y = Y;
  this->Z = Z;
}

VECTOR VECTOR::Add( VECTOR & V )
{
  //Addere to vektorer og returner resultatet
  return VECTOR( X + V.X, Y + V.Y, Z + V.Z, 1 );
}

VECTOR VECTOR::Sub( VECTOR & V )
{
  //Subtrahere to vektorer og returner resultatet
  return VECTOR( X - V.X, Y - V.Y, Z - V.Z, 1 );
}

VECTOR VECTOR::Mul( VECTOR & V )
{
  //Multiplicere to vektorer og returner resultatet
  return VECTOR( X * V.X, Y * V.Y, Z * V.Z, 1 );
}

double VECTOR::Dot( VECTOR & V )
{
  //Returner prik produktet af to vektorer
  return X * V.X + Y * V.Y + Z * V.Z;
}

void VECTOR::Cross( VECTOR & V1, VECTOR & V2 )
{
  //Find kryds produktet af to vektorer
  X =    V1.Y * V2.Z - V1.Z * V2.Y;
  Y = -( V1.X * V2.Z - V1.Z * V2.X );
  Z =    V1.X * V2.Y - V1.Y * V2.X;
}

double VECTOR::Magnitude( void )
{
  //Returnere magnituden
  return X * X + Y * Y + Z * Z;
}

double VECTOR::Length( void )
{
  //Returnere længden af vektoren
  return sqrt( Magnitude() );
}

double VECTOR::Length( VECTOR & V )
{
  //Returnere længden mellem to vektor
  return sqrt( ( X - V.X ) * ( X - V.X ) +
               ( Y - V.Y ) * ( Y - V.Y ) +
               ( Z - V.Z ) * ( Z - V.Z ) );
}

void VECTOR::Normalize( void )
{
  //Normaliser vektoren
  double L = Length();

  if ( L != 0.0 )
  {
    X = X / L;
    Y = Y / L;
    Z = Z / L;
  }
  else
    {
      X = 0;
      Y = 0;
      Z = 0;
    }
}

//Möller & Trumbore's klassiske algoritme fra: Journal of Graphic Tools, 1997
unsigned char VECTOR::Intersect( VECTOR & RayNear, VECTOR & RayFar, VECTOR & V1, VECTOR & V2, VECTOR & V3,
                                 const bool TwoSided,
                                 const double DepthTest )
{
  unsigned char Result = 0;
  X = 0;
  Y = 0;
  Z = 0;

  VECTOR E1;
  E1.X = V2.X - V1.X;
  E1.Y = V2.Y - V1.Y;
  E1.Z = V2.Z - V1.Z;

  VECTOR E2;
  E2.X = V3.X - V1.X;
  E2.Y = V3.Y - V1.Y;
  E2.Z = V3.Z - V1.Z;

  VECTOR P( RayFar.Y * E2.Z - E2.Y * RayFar.Z,
            RayFar.Z * E2.X - E2.Z * RayFar.X,
            RayFar.X * E2.Y - E2.X * RayFar.Y, 1 );

  double A = E1.X * P.X + E1.Y * P.Y + E1.Z * P.Z;

  //Tjek for precision
  if ( A > -0.00001 && A < 0.00001 )
  return 0;

  //Find ud af om bagsiden eller forsiden af trekanten skæres
  if ( !TwoSided && A < -0.00001)
  {
    //Bagsiden af trekanten er blivet skåret
    //men funktionen afsluttes fordi bagsiden ønskes at blive ignoreret!
    return 0;
  }
  else //Bagsiden af trekanten er blevet skåret
    if ( TwoSided && A < -0.00001 )
    Result = 2;
    else//Forsiden af trekanten er blevet skåret
      Result = 1;

  //Denne her division er langsom men kan ikke undværres!
  double F = 1.0 / A;

  VECTOR S( RayNear.X - V1.X,
            RayNear.Y - V1.Y,
            RayNear.Z - V1.Z, 1 );

  double U = S.X * P.X + S.Y * P.Y + S.Z * P.Z;
  U = U * F;

  //Find ud af om U er indenfor eller udenfor trekanten
  if ( U < 0.0 || U > 1.0 )
  return 0;

  VECTOR Q( S.Y * E1.Z - E1.Y * S.Z,
            S.Z * E1.X - E1.Z * S.X,
            S.X * E1.Y - E1.X * S.Y, 1 );

  double T = E2.X * Q.X + E2.Y * Q.Y + E2.Z * Q.Z;
  T = T * F;

  //Test dybden
  if ( T > DepthTest )
  return 0;

  double V = RayFar.X * Q.X + RayFar.Y * Q.Y + RayFar.Z * Q.Z;
  V = V * F;

  //Find ud af om V er indenfor eller udenfor trekanten
  if ( V < 0.0 || U + V > 1.0 )
  return 0;

  X = U; //X komponenten er en barycentric U koordinat
  Y = V; //Y komponenten er en barycentric V koordinat
          //Noté: For at få den barycentric W koordinat: W = 1 - U - V
  Z = T; //Z komponenten er afstanden mellen intersektions punkt and RayNear (Viewport)

  return Result;
}

void VECTOR::FollowLine( VECTOR & V1, VECTOR & V2, const double Distance )
{
  X = V1.X + ( ( V2.X - V1.X ) * Distance );
  Y = V1.Y + ( ( V2.Y - V1.Y ) * Distance );
  Z = V1.Z + ( ( V2.Z - V1.Z ) * Distance );
}

Hvad synes du om denne artikel? Giv din mening til kende ved at stemme via pilene til venstre og/eller lægge en kommentar herunder.

Del også gerne artiklen med dine Facebook venner:  

Karma barometer (30 dage)

IT jobs | Kontakt | Om Udvikleren.dk | Om karma | IT nyheds arkiv | Annoncering

X