Tags:    diverse

Matematik for 3D udviklere - vektorer

Inden folk begynder at hagle denne artikel ned samt mine matematiske færdigheder, vil jeg sige at jeg ikke har beskæftiget mig med denne type matematik tidligere. Jeg har indset at skal jeg lave noget fornuftigt 3D programmering i enten DirectX eller OpenGL så er jeg nødt til at kende lidt til matematik. Min Højere Handelseksamen med Matematik på B niveau rækker desværre ikke så langt som til at have gennemgået vektorer. Jeg håber denne artikel kan give lidt lys over det matematik jeg gennemgår. De helt store matematiske genier må bære over med mig ved at trække på smilebåndet over min manglende viden. Jeg ved at jeg nu har forståelse for dette område, og det hjælper mig meget i min daglige udvikling.

Hvad kan man bruge det til

Vektorregning er særdeles nyttigt når man arbejder med geometri eller trigonometri. Eksempelvis til at regne på forskellige lilniestykker i et koordinatsystem, men måske vigtigst af alt så bruges det hele tiden når man arbejder med 3D og spiludvikling.

Vektorer

En vektor kan meget simplistisk forklares som en linie i et koordinatsystem. Det der gør en linie til en vektor er at den har en længde og en retning. En vektors egenskaber består således at to ting, en længde og en retning. Mere er der egentligt ikke i vektorer. Dette er meget simpelt og ikke særligt svært.



Det betyder intet for en vektor om man taler om et almindeligt 2D miljø eller om et 3D miljø eller sågar et 4D miljø, en vektor består stadig kun af en længde og en retning. En vektors udgangspunkt (koordinater fra hvor den starter) betyder ikke noget for dens egenskaber, dette betyder med andre ord at alle vektorer der har ens længde og retning (det vil sige at de er parallelle) er lig med hinanden.



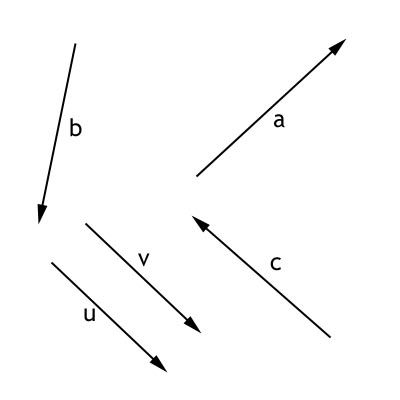
På billedet er vist 5 frit definerede vektorer.

Når en vektor befinder sig med dens "hale" i centrum af et koordinatsystem (dvs. 0,0) så siger man at den befinder sig i "Standard position". Det vil sige at har man en vektor der befinder sig i standard posistion så kan den beskrives ved at angive dens "hoved". Disse to koordinater kaldes for en vektors komponenteer, eller mere simplet for dens start og slut koordinater.



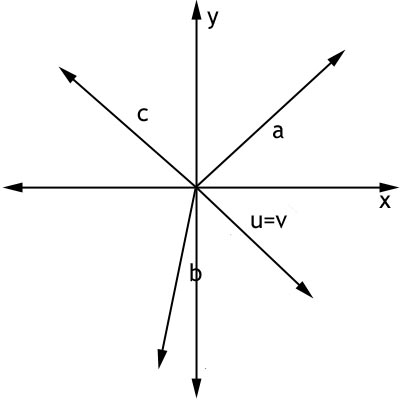
Som det kan ses har vi de to vektorer u og v lig med hinanden, dette skyldes at de har samme længde og retning, hvilket netop var forudsætningen for at man kunne sætte dem lig med hinanden. Da man kan definere en vektor, der er i standard position (dvs. har "hale" i centrum) blot ved at angive dens "hoved" kan man nemt forveksle punkter og vektorer. Punkter er kun et punkt i et koordinatsystem mens en vektor er længde og retning. Normalt angiver man en vektor med små bogstaver som der også tidligere er vist, men man kan også bruge store bogstaver. Her er nogle eksempler på 2, 3 og 4 dimensionelle vektorer:

implementeringer af vectorer:

C# eksempel

using System;

namespace Vectorer
{
                /// <summary>
	/// An implementation of a 3D vector
	/// </summary>
	public class Vector3
	{
		private float x;
		private float y;
		private float z;

		public Vector3(float newX, float newY, float newZ)
		{
			x = newX;
			y = newY;
			z = newZ;
		}

		public float X
		{
			get { return x; }
			set { x = value; }
		}

		public float Y
		{
			get { return y; }
			set { y = value; }
		}

		public float Z
		{
			get { return z; }
			set { z = value; }
		}
	}
}

Delphi eksempel

unit Vector3;

interface

type
  TVector3 = class
private
  a_x   : double;
  a_y   : double;
  a_z   : double;
public
  procedure Create(newx: double; newy: double; newz : double);
  property X : double read a_x write a_x;
  property Y : double read a_y write a_y;
  property Z : double read a_z write a_z;
end;

implementation

{ TVector3 }

procedure TVector3.Create(newx: double; newy: double; newz : double);
begin
  a_x := newx;
  a_y := newy;
  a_z := newz;
end;

end.

C++ eksempel

class Vector3
{
private:
	float a_x;
	float a_y;
	float a_z;
public:
	Vector3(float newx, float newy, float newz)
	{
		a_x = newx;
		a_y = newy;
		a_z = newz;
	}

	getX()
	{
		return a_x;
	}

	getY()
	{
		return a_y;
	}

	getZ()
	{
		return a_z;
	}

	setX(float newX)
	{
		a_x = newX;
	}

	setY(float newY)
	{
		a_y = newY;
	}

	setZ(float newZ)
	{
		a_z = newZ;
	}
};

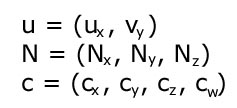
Det bogstav der står til venstre for ligheds tegnet er navnet på vektoren. De bogstaver der står inden i paranteserne er punkterne for denne vektor i de forskellige dimensioner. Det vil sige at de steder der står ux (læs det x som sænket i forhold til u) er vektorens koordinat på x aksen og så fremdeles med de andre punkter på deres respektive akser. Det vil også sige at når man angiver en vektor så skriver man et tal på pladsen i vektorens beskrivelse i stedet for eks. ux. Dette er et eksempel på en vektor der går igennem 1 på x-aksen, 2 på y-aksen og 3 på z aksen (dvs. en tredimensionel vektor).

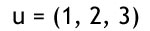
Fire typer vektorer

Der introduceres nu fire typer vektorer, den første er en nul-vektor. Denne vektor har nul som alle punkter i dens definition:



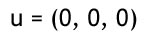
De tre sidste typer kaldes for basis vektorer for de løber langs deres respektive akser (x,y,z) og har en længde på 1:



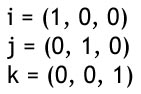
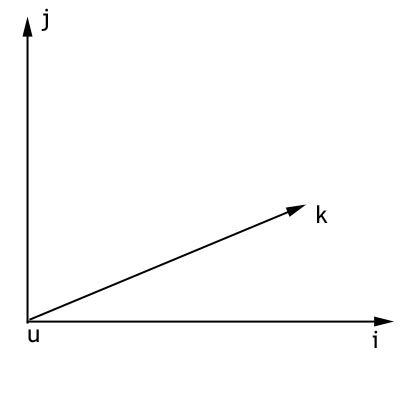
dette vil rent grafisk faktisk danne et tredimensionelt koordinatsystem, som det nedenstående:



Rent geometrisk siger man at to vektorer er ens hvis deres retning og længde er ens. Rent algebraisk siger man at to vektorer er ens hvis deres længde er ens og deres tilsvarede komponenter er ens (dvs. x i den ene skal være lig med x i den anden):



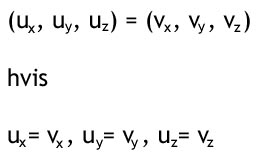
Typisk når man programmerer vælger man at repræsentere en punkt i et koordinatsystem med en floating point værdi (float/kommatal). Derfor kan man godt risikere at man sammenligner to tal der burde være forskellige, men på grund af afrundinger ikke er det. For at kunne sammenligne disse definerer man en "buffer" værdi kaldes EPSILON. Denne værdi er meget lille og skal egentligt bare udjævne de små forskelle vi løber ind i ved afrundinger og andet Det vil

sige at skal vi teste om to vektorer er ens så trækker vi deres koordinater (indenfor hver dimension/akse) fra hinanden og er restværdien mindre end EPSILON, så er de ens.

C++ eksempel

const float EPSILON = 0.001f;
bool equals(float x, float y)
{
	return abs(x-y) < EPSILON ? true : false;
}

C# eksempel

const float EPSILON = 0.001f;
private bool equal(float x, float y)
{
	float difference;
	difference = Math.Abs(x-y);
	if(difference<EPSILON)
	{
		return true;
	}
	else
	{
		return false;
	}
}

Delphi eksempel

function equals(x, y :double): boolean;
var
  EPSILON : double;
begin
  Result:=false;
  EPSILON:=0.001;
  if (abs(x-y) < EPSILON) then
  begin
        Result:=true;
  end;
end;

Længden på en vektor

Rent matematisk kan man beregne længden på en vektor ved at benytte nedenstående formel:



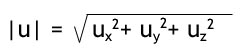
Linierne omkring u'et betyder "længden af", og i dette tilfælde u.

Eksempel:
Find længden af nedenstående vectorer:

u = (1, 2, 3)
v = (1, 2)

Ved hjælp af ovenstående formel kan vi nu beregne længden af hver vektor. Vi starter med vektor u:



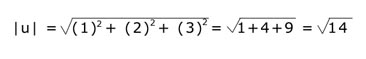
og herefter vektor v:

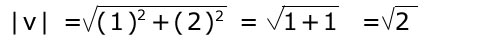
Normalisering af vektorer

Ved at normalisere en vektor forstås at man transformerer den således at dens længde bliver til 1. Dette kaldes også for en enhedsvektor. Denne normalisering ka beregnes ved at dividere længden på vektoren op i hvert enkelt element således:



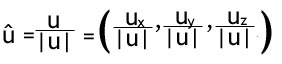
Et bogstav med en hat ^ over betyder normalisering. Nu er det så bare at indsætte tal i formlen og derefter er vektoren normaliseret.

Vektor addering

Man kan lægge to vektorer sammen ved at addere deres respektive korrodinater sammen, det vil sige at alle fra x dimensionen lægges sammen, det samme gør sig gældende for alle elementer fra y dimensionen og så videre.

Eksempel:



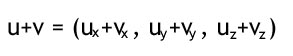
Når man lægger to vektorer sammen kan det se ud som dette. Det der er sket er at man "forlænger" den ene vector med den anden (symboliseret med den grå linie, det er reelt vektoren v der er langt i enden på vektoren u).

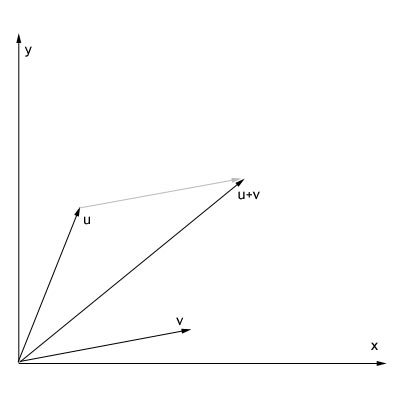
Subtraktion af vektorer

Ganske som ved addering trækker man to vectorer fra hinanden ved at trække deres respektive koordinater/punkter fra hinanden, formelen er ikke meget anderledes end ved addering, der står blot minus - i stedet for plus +.



Ved at trække to vektorer fra hinanden får vi som resultat en vektor der peger fra spidsen af v til spidsen af u. Dette bruges tit i computer spil til at beregne en retning fra et punkt til et andet.

Multiplikation af vektorer

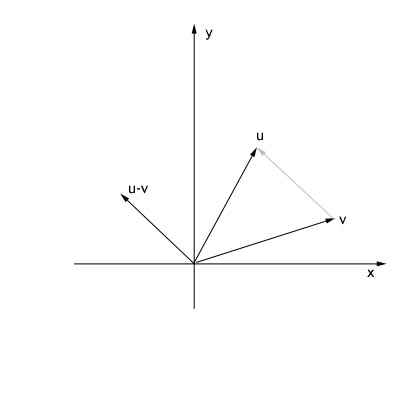
Ved at gange to vektorer sammen bevares retningen men længden forøges i henhold til den faktor der ganges med. Hvis der ganges med en negativ faktor så flippes vektoren.

Eksempel:

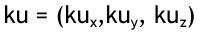
Prik produkter

Prikprodukter er et af to produkter der er defineret i vektor algebra, det bliver beregnet på følgende måde:



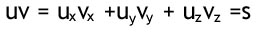
Denne formel giver ingen umiddelbar geometrisk mening, men ved at bruge cosinus' lov kan vi finde en sammenhæng



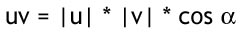
Denne regel siger at prikproduktet mellem to vektorer er lig cosinus til vinklen mellem dem, skaleret med vektorernes længder. Det vil sige at hvis begge vektorer er unit vektorer (dvs med en længde på 1) så er u gange v lig med cosinus til vinklen mellem dem. Nogle nyttige tips til dette forhold er disse:

Hvis U * v = 0 så er u retvinklet på v.
Hvis U * v > 0 så er vinklen mellem de to vektorer større end 90 grader
Hvis u * v < 0 så er vinklen mellem de to vektorer større end 90 grader.

Krydsprodukter

Den anden form for multiplicering er krydsprodukter. Ulig prikproduktet der giver en længde forøgelse giver krydsproduktet derimod en ny vektor ud fra de eksisterende vektorer. Denne nye vektor er vinkelret på både vektoren u samt vektoren v. Det vil med at dre ord sige at krydsproduktet af vektorerne u og v giver en anden vektor p, der er vinkelret på begge vektorer. Krydsproduktet bliver beregnet således:



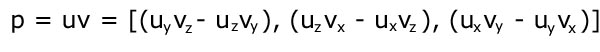
I komponentform vil dette se således ud:



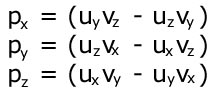
Rent geometrisk ville det blive afbildet således:



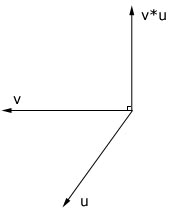
Et eksempel på dette kunne for eksempel være at man skal finde krydsproduktet af to vektorer k og i og bagefter verificere at den nye vektor j rent faktisk står vinkelret på dem begge:



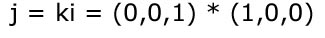
Dette bliver læst på følgende måde (de ekstra paranteser er for ikke at forvirre når man ganger sammen)



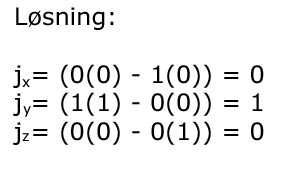
Dette betyder at den nye vektor j ser således ud:



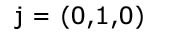
Og som der tidligere er blevet gennemgået så kan vi nu kontrollere at den nye vektor rent faktisk er vinkelret på de andre to vektorer, dette kunne vi teste ved at gange dem sammen og hvis resultatet var nul så var de vinkelrette på hinanden. Det vil sige at j*k=0 og j*i=0. Dette giver os det endelige bevis.

Hvad synes du om denne artikel? Giv din mening til kende ved at stemme via pilene til venstre og/eller lægge en kommentar herunder.

Del også gerne artiklen med dine Facebook venner:  

Karma barometer (30 dage)

IT jobs | Kontakt | Om Udvikleren.dk | Om karma | IT nyheds arkiv | Annoncering

X